04/17/2008
Overview
Here we designate by Game Engine the set of high-level rules that are used to simulate a virtual world, manually (table-top games with a real Game Master) or, more importantly here, with the help of a computer (notably in the case of a video game, with an emulated Game Master).
Concerns like rendering, input handling, etc. are deemed outside of the scope of the game engine: if the game was a networked one, we would focus here on the server-side simulation of the game actors only.
Our goal here is to define:
- what are the general requirements for most Role-Playing Games regarding the underlying game engine
- what is the solution we preferred to apply to fulfill these needs, and why
We based our system on the one HirinkaŽl described here (in French), most choices and remarks regarding the evaluation of actions are just taken from this document, adapted a bit and translated.
Place of random
We chose to introduce some randomness when resolving actions, as it creates a kind of "dramatic tension". It forces oneself to evaluate every possible outcome and to ponder them painfully.
Realistic versus epic setting
Depending on the interactive story to be told, some actions might be totally impossible or, only, very unlikely (this is a difference of nature). The more unlikely outcomes may happen, the most epic the story will be. We prefer to keep a certain level of "epicness", should such word exist.
Resolving actions
What for ?
In a game, the success of all kinds of attempts of actions have to be evaluated, like when:
- attacking a foe
- parrying an attack
- climbing a wall, etc. The game system has to choose whether each action succeeds or fails.
How ?
It is done by evaluating the probability p of success (say, between 0 and 100%), and drawing a random value r in, [0,100]. If r<p, then the action succeeds, if r>p it fails, otherwise r=p and the outcome is neither a success nor a failure (for the sake of simplicity we will consider from now on that the action is then a success).
The core of the problem is to have the game system select an accurate, realistic value for p, the probability of success for that specific action.
The intended outcome of this part of the rule system is not a predetermined "one size fits all" probability of success: we want a probability that matches closely the set of specific and hardly predictable circumstances that exist at this moment of the game.
As the game creator cannot precompute all the possible contexts (as they are too numerous, due to the combinatorial explosion of possible in-world variations), the game system has to rely on rules that can determine on the fly, in the light of a specific context, a global probability of success.
We chose to rely on HirinkaŽl's system because:
- it can easily take into account all kinds of situations
- it is logical, consistent, symmetrical and fair
- it is original
- it is quite simple to understand and use
- it can be used both in video games (thus being computer-based) and in table-top games (with dice and an abacus)
The reason we like this system lies mainly in the first advantage listed (flexibility, adaptability), as it offers us a way of adapting to an actual situation (real-life, complex, full of context) the chances of success of a given action which was modelled under normal circumstances (nominal conditions) only.
Two inputs: base probability & modifiers
Let's take, from the document we just mentioned, the example of a character wanting to attack another, and let's suppose we can evaluate the base probability, i.e. the probability of success of this action under normal circumstances.
The problem is that, in real cases, we are never in that stereotypical situation: the characters might be fighting in the dark, or one may be wounded, or there may be multiple opponents, etc. How to obtain, from the probability evaluated under normal circumstances, a custom probability reflecting all these numerous elements of context ?
What we really need actually is to be able to take into account probability modifiers that:
- can be defined once for all, not depending on the base probability nor on any other modifier
- can convert the base probability into the target context-dependent probability realistically (ex: it must be more difficult indeed to hit when wounded) and correctly (ex: probabilities must remain in the [0,1] range)
One output: the actual context-dependent probability
To handle modifiers we retained the function suggested in the aforementionned paper:
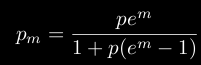
This function, when given a base probability (p, abscissa) and a modifier (m, select the corresponding curve), determines the resulting modified probability (pm, ordinate):

The wider curves, representing modifiers of -50%, 0% and 50%, allow to find easily the curves for intermediate modifiers, as they are paced every 10%.
One can see the symmetry of modifiers: the value of the increase in probability due to a given modifier p is equal to the value of the decrease in probability due to a modifier of -p.
The probability-modifier.py script gives some more indications:
For a base probability of success of 0.0 %, with a modifier of: -30.0 %, modified probability is 0.0 %. -20.0 %, modified probability is 0.0 %. -10.0 %, modified probability is 0.0 %. 0.0 %, modified probability is 0.0 %. 10.0 %, modified probability is 0.0 %. 20.0 %, modified probability is 0.0 %. 30.0 %, modified probability is 0.0 %. For a base probability of success of 25.0 %, with a modifier of: -30.0 %, modified probability is 8.63 %. -20.0 %, modified probability is 12.5 %. -10.0 %, modified probability is 17.9 %. 0.0 %, modified probability is 25.0 %. 10.0 %, modified probability is 33.6 %. 20.0 %, modified probability is 43.5 %. 30.0 %, modified probability is 54.0 %. For a base probability of success of 50.0 %, with a modifier of: -30.0 %, modified probability is 22.0 %. -20.0 %, modified probability is 30.1 %. -10.0 %, modified probability is 39.6 %. 0.0 %, modified probability is 50.0 %. 10.0 %, modified probability is 60.3 %. 20.0 %, modified probability is 69.8 %. 30.0 %, modified probability is 77.9 %. For a base probability of success of 75.0 %, with a modifier of: -30.0 %, modified probability is 45.9 %. -20.0 %, modified probability is 56.4 %. -10.0 %, modified probability is 66.3 %. 0.0 %, modified probability is 75.0 %. 10.0 %, modified probability is 82.0 %. 20.0 %, modified probability is 87.4 %. 30.0 %, modified probability is 91.3 %. For a base probability of success of 100. %, with a modifier of: -30.0 %, modified probability is 100. %. -20.0 %, modified probability is 100. %. -10.0 %, modified probability is 100. %. 0.0 %, modified probability is 100. %. 10.0 %, modified probability is 100. %. 20.0 %, modified probability is 100. %. 30.0 %, modified probability is 100. %. For a base probability of success of 60.0 %, with first modifier being 20.0 %, with second modifier being 15.0 %, modified probability is 86.7 %. For a base probability of success of 60.0 %, with first modifier being 15.0 %, with second modifier being 20.0 %, modified probability is 86.7 %. For a base probability of success of 60.0 %, with a modifier of 35.0 %, modified probability is 86.7 %.
We can see that if the base probability is 100% or 0%, the action will be always respectively a success or a failure, not depending on the modifier.
Moreover, multiple modifiers can be applied, applying m1 then m2 results in the same as applying m2 then m1, which is (in practice) the same as applying directly m3 = m1 + m2.
How to choose the rule inputs ?
If determining the base probability is part of the usual tasks of the seasoned Game Master, modifiers, as used here, are specific to this system.
The numerical rules have been calibrated so that, when base probability is at 50%, a modifier equal to m will result in a final probability equal to about 50+m %.
So, to evaluate the value of a modifier modelling a specific element of context, the Game Master just has to imagine the case where:
- we are under normal circumstances
- and the action is to be performed by a candidate who has 50% of chance of succeeding, 50% of chance of failing
Then, should the studied element of context occur, what would be the new probability of success (pnew) ? Once that value has been evaluated by the Game Master, the modifier is just equal to that value minus 50%: m = pnew - 50%.
More precisely, the previous numerical recipe (50+m %) is an approximation, mostly accurate for small values of m. The real relation is: if the Game Master chooses, for the aforementioned probability of success, pnew, then m = 1 / (1+ exp(-pnew)).
It leads to this abacus, helping to evaluate this modifier:
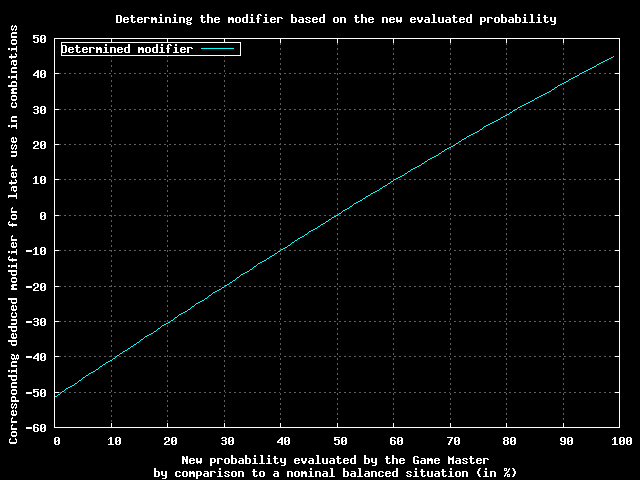
We can see that in most situations it is perfectly safe to stick to m = pnew - 50%.
Let's take an example
Let's suppose that a given dark ninja has a nominal probability of climbing a given wall successfully equal to 80% (ninjas are somewhat gifted for that kind of exercise). Let's suppose as well that we are at night (note that it is a bonus for our dark ninja) but it is raining (malus) and sadly he has just been wounded by an alligator (big malus).
As modifiers are made to be context-free, we need here to evaluate only the impact of a given modifier against the nominal situation, without having to bother with any other modifier (we suppose here all modifiers are independent, although one may argue it is an oversimplification here).
Let's take the malus due to the wound. We may consider that a wounded dark-ninja at daylight, dry weather, incures a 35% penalty when trying to climb that kind of wall.
The same exercise may result in a 10% bonus for the climbing of an unwounded ninja, dry weather, but in the night, and in a 5% malus for the climbing of an unwounded ninja, during the day, but under the rain.
So, what is the overall probability of successful climbing, for our wounded ninja under the rain at night time ? Modifiers have to be summed, it results in a global modifier of -35+10-5=-30. We then look at our curves: the intersection of the ninja base probability of success (80%) with the curve of the -30% modifier gives us a final probability of about 53%. 0ur ninja finally has little more chance to arrive at the top of the wall than to fall miserably in the flowers.